Ever wondered how machines learn to play chess, predict the weather, or recommend your next favorite song? The secret lies in a treasure trove of mathematical theorems that provide the backbone for these AI miracles. Let’s decode these powerful principles with engaging examples and see how they apply to our fascinating AI endeavors!
Statistical Foundations: Mastering the Art of Prediction
Central Limit Theorem (CLT) 🎲
Ever wonder why we trust polls during election season? Thanks to the Central Limit Theorem (CLT), we know that the averages of samples (like polling data) will typically resemble a normal distribution, giving us reliable predictions from random samples.
Python Example: Predicting Soccer Match Outcomes
Let’s say we want to predict the average goals scored in soccer matches. We can simulate this using Python and visualize how the sample means approach a normal distribution.

In this code, we simulate the goals scored in soccer matches using a Poisson distribution and demonstrate how the sample means form a normal distribution, validating the Central Limit Theorem.
Law of Large Numbers (LLN) 📈
Think of the Law of Large Numbers (LLN) as the reason we get better at guessing the outcome of a flipped coin the more times we flip it. This theorem guarantees that as more data is collected, the average of the results reflects the true underlying probability.
Python Example: Estimating Goal Average
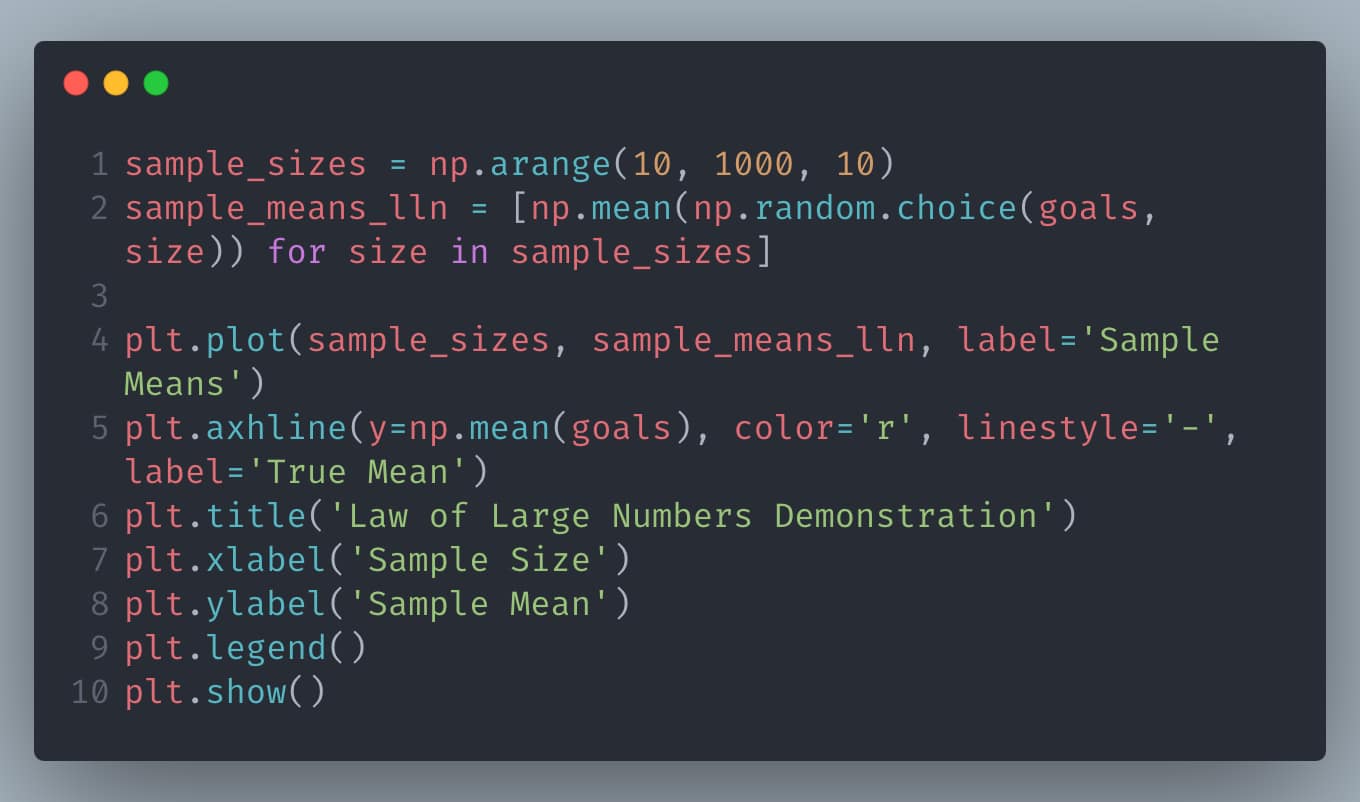
This example shows how the sample mean of soccer goals converges to the true mean as the sample size increases, illustrating the Law of Large Numbers.
Bayes’ Theorem 🔍
It’s like updating your beliefs after binge-watching a new TV show. If you initially think you’ll hate it but end up enjoying the first few episodes, Bayes’ Theorem helps revise your prediction on whether you’ll like the next season based on this new evidence!
Python Example: Updating Predictions with New Data
Suppose we want to update our belief about a soccer team’s chance of winning after observing their performance in the first few matches.

In this code, we calculate the updated probability that a team will win based on new performance data, applying Bayes’ Theorem.
Neural Network Capabilities: Building Brains in Silicon
Universal Approximation Theorem 🌍
Imagine teaching a robot to recognize pets. This theorem assures us that a neural network can learn to distinguish cats from dogs, no matter how quirky the breeds, as long as it’s designed with enough complexity.
Python Example: Simple Neural Network for Classification

This example demonstrates a simple neural network using the Universal Approximation Theorem to classify data, showcasing its ability to model complex functions.
Kolmogorov-Arnold Theorem 🧬
This is like breaking a complex recipe into steps so simple even a novice chef can follow. In AI, it means decomposing a difficult problem (like navigating a maze) into simpler tasks (turn left, move forward).
Optimization and Complexity: Fine-Tuning the AI Engine
Hoeffding’s Inequality 📐
This gives us the confidence to use small datasets to make big decisions, like choosing the best headline for an ad campaign, by quantifying how likely our choice is to perform well overall.
Python Example: Confidence Intervals with Small Samples
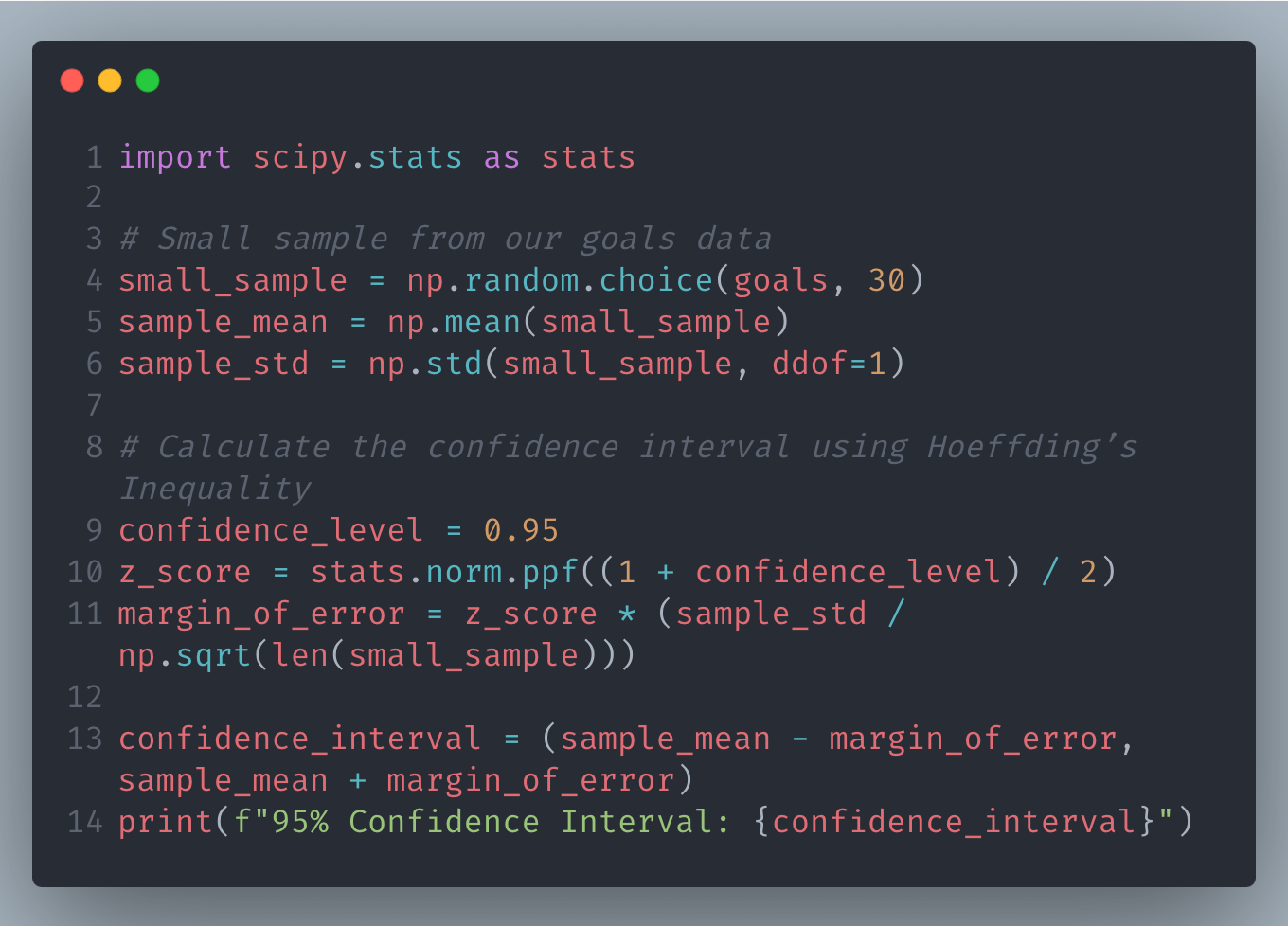
This code calculates a confidence interval for the average goals scored using a small sample, leveraging Hoeffding’s Inequality.
PAC Learning 🎯
Provides a playbook for ensuring our AI models perform well in the real world, not just in the lab, by telling us how much data we need to train them effectively.
Data Transformation and Representation: Seeing the Forest for the Trees
Mercer’s Theorem 🌐
Behind every successful image recognition tool is a kernel trick, transforming complex images into a format where they can be easily classified, all thanks to Mercer’s insights.
Singular Value Decomposition (SVD) 🧩
It’s like condensing an encyclopedia into a pamphlet without losing the essence. SVD helps us simplify massive datasets into something manageable, enhancing everything from recommendation systems to search engines.
Python Example: SVD for Dimensionality Reduction
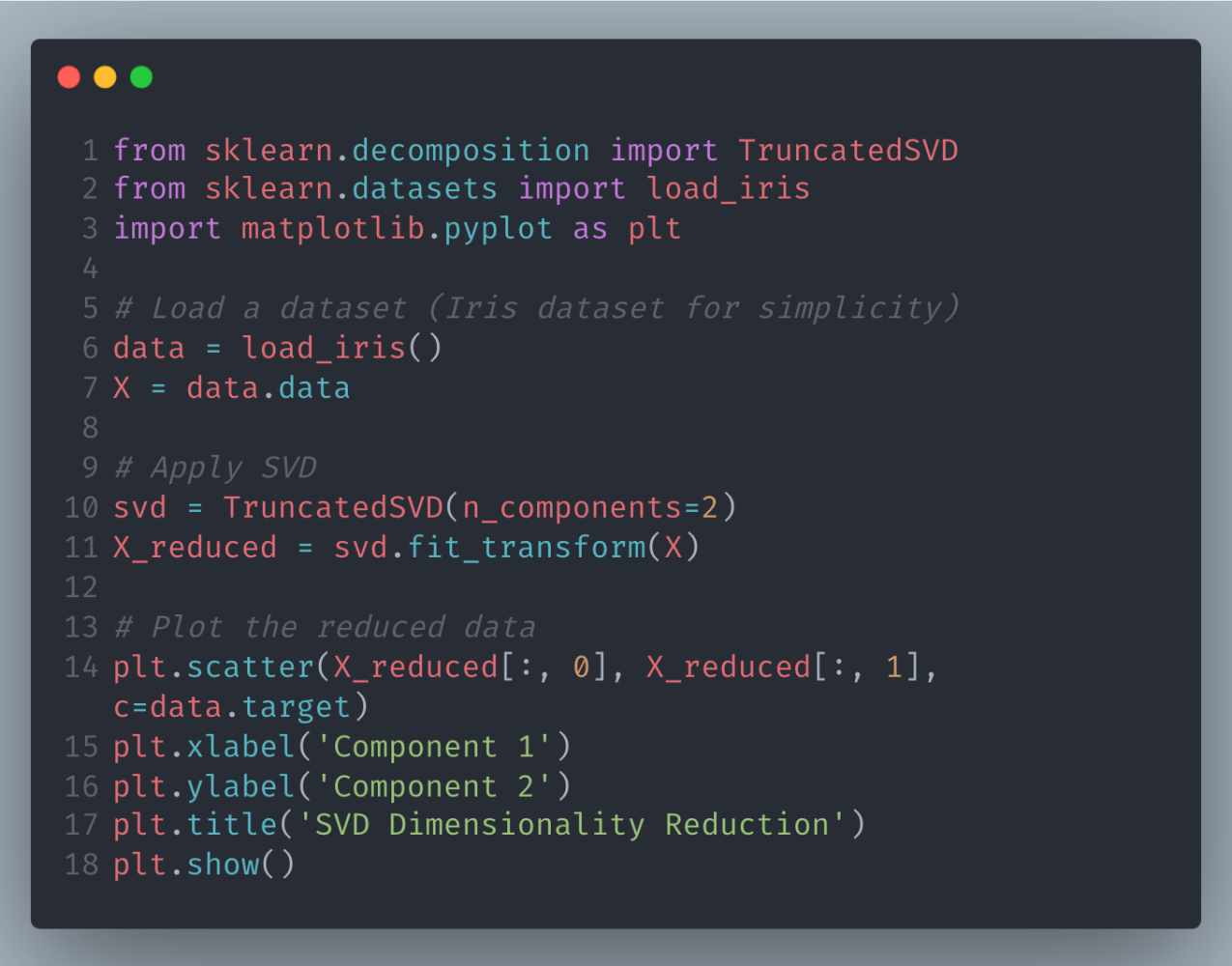
This code uses Singular Value Decomposition to reduce the dimensionality of the Iris dataset, making it easier to visualize and analyze.
Gaussian Process Theorems 🌌
These are the crystal balls of machine learning, letting us predict future trends with a level of uncertainty, whether forecasting stock movements or planning delivery routes under varying conditions.
Python Example: Gaussian Process Regression
This example demonstrates Gaussian Process Regression to predict future trends with a measure of uncertainty.
Conclusion
These mathematical principles not only fuel the engine behind AI’s capabilities but also provide a structured pathway to innovate and apply these technologies effectively. By understanding and applying these theorems, we unlock the potential to solve real-world problems with AI, pushing the boundaries of what machines can learn and achieve.

FAQ
1. What is the Central Limit Theorem (CLT) and why is it important in AI?
- The Central Limit Theorem (CLT) states that the distribution of sample means approximates a normal distribution as the sample size becomes larger, regardless of the population’s distribution. In AI, this theorem supports the reliability of predictions made from large datasets, ensuring that statistical methods like hypothesis testing remain robust and valid.
2. How does the Law of Large Numbers apply to machine learning?
- The Law of Large Numbers (LLN) ensures that as more data is collected, the computed averages of these data will converge to the expected value or true mean. In machine learning, this means that models become more accurate and stable as they are trained on increasingly larger datasets.
3. Can you explain Bayes’ Theorem and its relevance to AI?
- Bayes’ Theorem allows for the update of probability estimates as new data becomes available. It is fundamental in many AI applications, such as spam filtering and diagnostic systems, where it helps to refine predictions based on new, incoming information.
4. What is the Universal Approximation Theorem?
- The Universal Approximation Theorem states that a feed-forward network with a single hidden layer containing a finite number of neurons can approximate continuous functions on compact subsets of 𝑅𝑛Rn, under mild assumptions about the activation function. This theorem is crucial for neural network design, indicating that neural networks have the capacity to model any complex function.
5. What role does the Kolmogorov-Arnold Theorem play in AI?
- The Kolmogorov-Arnold Theorem provides a foundation for decomposing complex multi-dimensional functions into sums of simpler functions, which is particularly useful in reducing the complexity of problems in AI by breaking them down into more manageable sub-problems.
6. What is Hoeffding’s Inequality and how is it used in AI?
- Hoeffding’s Inequality provides a bound on the probability that the sum of random variables deviates from its expected value. In AI, this is used to assess the reliability of results derived from small data samples, ensuring that decisions or predictions are statistically sound.
7. Explain PAC Learning in simple terms.
- Probably Approximately Correct (PAC) Learning is a framework that defines the conditions under which a learning algorithm will perform well. It quantifies how much data is needed to ensure that a model trained on this data will generalize well to new, unseen data, which is essential for developing robust AI systems.
8. How does Mercer’s Theorem support machine learning?
- Mercer’s Theorem is the basis for kernel methods used in machine learning for tasks like classification and regression. It explains how complex data can be transformed into a higher-dimensional space to make it linearly separable, which is pivotal for algorithms like Support Vector Machines.
9. What is Singular Value Decomposition and its application in AI?
- Singular Value Decomposition (SVD) is a method of decomposing a matrix into its constituent elements, which are used to reduce dimensionality, improve computational efficiency, and remove noise from data. In AI, SVD is instrumental in building recommendation systems and enhancing image processing techniques.
10. Describe Gaussian Process Theorems and their use in predictive modeling.
- Gaussian Process Theorems underpin the Gaussian Process models in machine learning, which provide a probabilistic approach to forecasting. These models are highly beneficial for making predictions that include a measure of uncertainty, useful in fields like finance and robotics for risk assessment and planning.
By integrating these mathematical theorems into AI models, we can create powerful, reliable, and innovative solutions that push the boundaries of what is possible with artificial intelligence.
Thanks for reading this article!